Solving Trigonometry the programmer way
This post contemplates me, stupidly solving a fairly difficult Trigonometry problem, the programmer way.
The problem
I stumble upon the problem on
Mind Your Decisions’ blog.
The question is: “What is the value of x?”
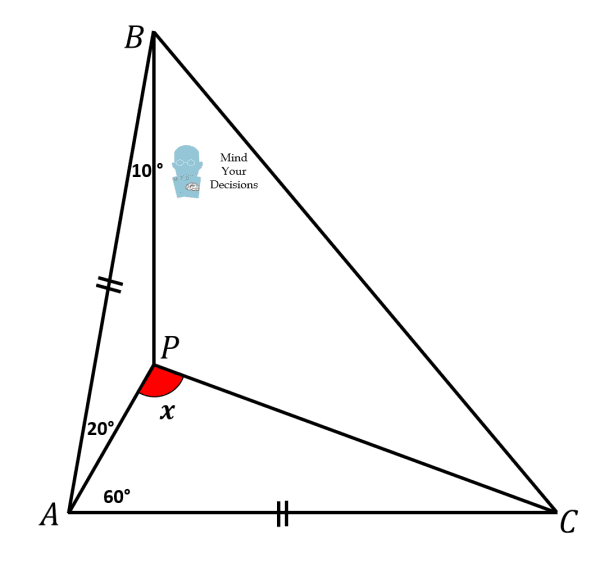
Initial attempt
At first, I tried everything I know. I wrote multiple complex equations on a text editor.
For instance:
area equation:
(AC * sin(ACB) * 2) * (AC * cos(ACB)) / 2 = (AB * AP * sin(BAP) / 2) + ((AC * cos(ACB) * 2) * (BP * sin(CBP)) / 2) + (AC * AP * sin(CAP) / 2)
known variables:
AB = AC = unit
ACB = 50 degrees
BAP = 20 degrees
CBP = 40 degrees
CAP = 60 degrees
result equation:
unit * sin(50) * unit * cos(50) = (unit * ap * sin(20) / 2) + (unit * cos(50) * bp * sin(40)) + (unit * ap * sin(60) / 2)
As I was writing more equations, I ended up with more variables. They are so overwhelming and seemingly impossible for me to solve.
I encourage you to try it yourself, it is harder than it looks.
Something is missing
I remembered studying a lot of Trigonometry in high school. And by “study”, I mean, noticing its existence in the school.

In my high school, nobody cares about how well a student performs, or how crappy (some) teachers and learning materials are.
It is quite a laid back lifestyle for me back then.
I was automatically passed, remembering that I did not study or knowing shit about Trigonometry beyond the definitions of sin, cos, tan functions.
Now I am not really that smarter than the past, but maybe, a smartass.
Looking at the problem again.

Data at the ABP triangle should be self-completed, given that we already know the values of every angle of the triangle.
In theory, every unknown parameter should be derivable from what we already knew.
The only possibility that made me unable to find the length of AP, from the available information alone, is because I lack some crucial knowledge.
Google to the rescue
After some Googling, YouTube watching, and Wikipedia browsing, I found the missing theorems. They are “the law of sines” and “the law of cosines”.
There are 2 possibilities about you:
- You are, like me, not knowing shits
Don’t worry; we’ll learn about them together. - You already know about the theorems
In this case, I think this post will be quite boring for you. I guess your life has many more things to do with Mathematics already. I’d recommend you move on to something else.
How much do you know about the Pythagorean theorem?
Most people know what it is; most people know its equation.
c^2 = a^2 + b^2
(Sorry I don’t install LaTeX renderer yet. Too lazy because I barely write anything about Mathematics)
But do you know how did they come up with the theorem?
Or, do you know the prove?
If your answer is “no”, exactly! That is what the theorems are for.

Theorems are just like software libraries.
If you wanted to work on a theorem, you have to know about it very well.
However, for the general public, even if you don’t know about a theorem that deep, you are free to utilize it (and make a citation) despite not knowing its every little detail.
The law of cosines: the generic Pythagorean theorem
Given the triangle below
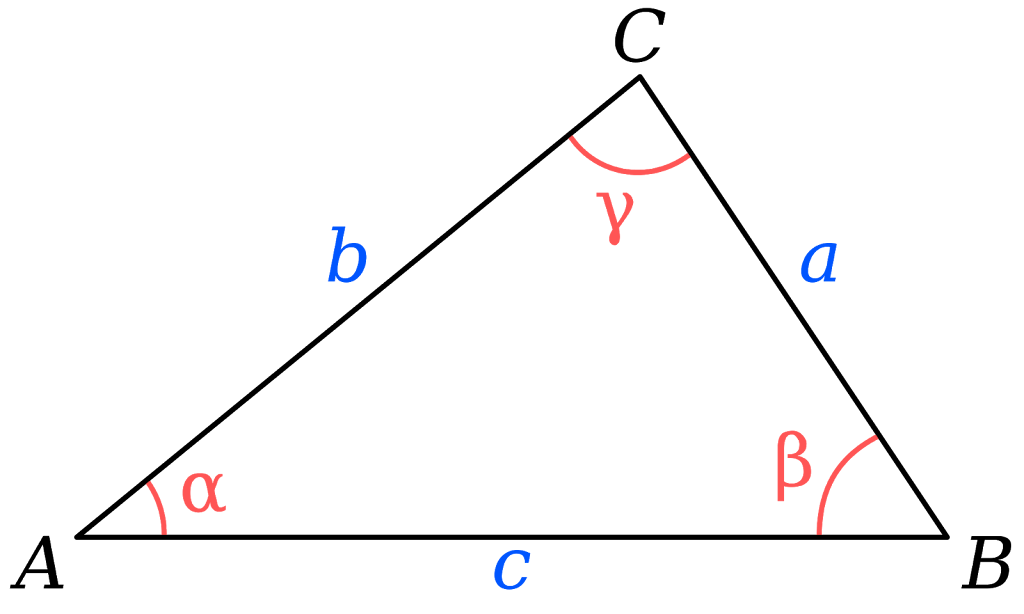
Pythagorean theorem works, if and only if, one of the angles is a right angle.
The law of cosines works regardless. In fact, the equations of both theorems look almost identical.
c^2 = a^2 + b^2 - 2ab * cos(gamma)
-2ab * cos(gamma) is there, sitting invisibly in the Pythagorean theorem too.
The law of sines: complements the cosines counterpart
One issue with the law of cosines is:
it only works when you know a set of adjacent side-angle-side of a triangle.
It does not work with the ABP triangle we are solving.
There is a counterpart that complements the law of cosines.
The equation is symmetric and quite easy to remember.

a/sin(alpha) = b/sin(beta) = c/sin(gamma)
Even if I have no idea how did they come up with this. It only requires a good-night sleep for me to commit it to my long-term memory.
Solving the problem
I think we can find the length of AP now with the newly learned theorems.

I’ll solve it in Ruby’s IRB, for convenience.
Interactive Ruby (aka IRB) is like the Jupyter Notebook Python people love.
It is the default REPL for Ruby suitable for quick calculation like this.
IRB is a bit better because it is installed by default with Ruby runtime. So it is more ubiquitous,
and it is arguably easier to bring up.
Starting with the law of sines.
def d2r(degrees)
degrees * ::Math::PI / 180
end
# math: ap / sin(10) = ab / sin(180 - 10 - 20)
# math: ap = ab * sin(10) / sin(180 - 10 - 20)
ap = 1.0 * ::Math.sin(d2r(10)) / ::Math.sin(d2r(180 - 10 - 20))
# result: ap = 0.3472963553338607
Great!
Now, find x
def r2d(radians)
radians / ::Math::PI * 180
end
# math: cp^2 = ap^2 + ac^2 - (2 * ap * ac * cos(60))
# math: cp = sqrt(ap^2 + ac^2 - (2 * ap * ac * cos(60)))
cp = ::Math.sqrt((ap ** 2) + 1 - (2 * ap * 1) * ::Math.cos(d2r(60)))
# result: cp = 0.8793852415718166
# math: sin(x) / ac = sin(60) / cp
# math: sin(x) = ac * sin(60) / cp
# math: x = arcsin(ac * sin(60) / cp)
x = ::Math.asin(1 * ::Math.sin(d2r(60)) / cp)
# result: x = 1.396263401595464
but the result x is wrong. We can notice it right away with keen eyes.
Because x is less than PI/2, which contradicts what we see in the rough but accurate sketch provided.
Upon consulting Ruby docs, we’ll know that the codomain of the arcsin implemented is between
[-PI/2, PI/2]; means the function won’t return a value greater than PI/2.
For now, I’ll just hack my way through by shifting the codomain of the arcsin from the standard library.
From [-PI/2, PI/2] to [PI/2, 3PI/2]
x = ::Math.asin(1 * ::Math.sin(d2r(60)) / cp * -1) + ::Math::PI
# result: x = 1.745329251994329
# result: r2d(x) = 99.99999999999999
r2d(x) is practically 100 degrees.
Avoiding arcsin
In theory, arcsin and arccos are indifferent.
But for our practical use case, arccos has better codomain characteristics,
spanning between [0, PI],
just the right range to calculate an angle of a triangle.
By tweaking the program a bit, we can calculate x accurately.
Using the law of cosines:
# math: ac^2 = ap^2 + cp^2 - (2 * ap * cp * cos(x))
# math: (2 * ap * cp * cos(x)) = ap^2 + cp^2 - ac^2
# math: cos(x) = (ap^2 + cp^2 - ac^2) / (2 * ap * cp)
# math: x = arccos((ap^2 + cp^2 - ac^2) / (2 * ap * cp))
x = ::Math.acos(((ap ** 2) + (cp ** 2) - 1) / (2 * ap * cp))
# result: x = 1.74532925199433
Putting all snippets together we’ll get
def d2r(degrees)
degrees * ::Math::PI / 180
end
def r2d(radians)
radians / ::Math::PI * 180
end
ap = 1.0 * ::Math.sin(d2r(10)) / ::Math.sin(d2r(180 - 10 - 20))
cp = ::Math.sqrt((ap ** 2) + 1 - (2 * ap * 1) * ::Math.cos(d2r(60)))
x = ::Math.acos(((ap ** 2) + (cp ** 2) - 1) / (2 * ap * cp))
# additional printing code only
formatted = r2d(x).then do |value|
round_9 = value.round(9)
next round_9 if round_9 == value.round(2)
value
end
puts "result: #{formatted}"
# result: 100.0
Lesson learned
Well, I learned
- 2 new theorems
- Trigonometry is not my thing, too stupid in this area perhaps
- Be careful of codomain when program something related to Trigonometry.
Apologize for the self-centered post
There are more interesting things I wanted to post.
Majorities of content on this site are more unique than this one.
I just feel like rediscovered something I should know a decade ago.
Please look around for more interesting stuff.